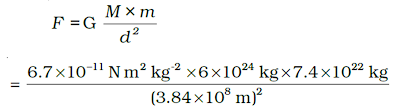👉 View PDF
Chapter 9: GRAVITATION
- Gravitation is a natural phenomenon by which objects with mass are attracted to each other.
-
The force
of attraction between two objects with mass due to gravitation is called the gravitational
force. E.g., falling of an object towards the earth, rotation of planets around
the Sun, rotation of moon around the earth etc. are due to gravitational force.
-
This was
first discovered by Isaac Newton.
GRAVITATION
-
Isaac Newton proposed that an apple and the moon are attracted to
the earth by same type of force.
-
He argued
that the moon, at each point of its orbit, falls towards the earth, instead of moving
in a straight line. So, it must be attracted by the earth.
Activity
•
Tie a
stone to a piece of thread and whirl it around.
•
The stone
moves in a circular path.
•
Release
the thread. The stone moves in a straight line, tangential to the circular path.
-
Without this
force, the stone moves in a straight line, tangential to the circular path.
-
The moon's motion around the earth is due to
centripetal force from the attraction of the earth. Without this force, the moon would move in a uniform
straight line.
-
According
to the third law of motion, the apple attracts the earth. But according to
the second law of motion, acceleration is inversely proportional to the mass
(F = ma). The mass of an apple is negligible compared to the earth. So,
the earth doesn’t move towards the apple. Similarly, the earth does not move
towards the moon.
-
Newton
concluded that all objects in the universe attract each other. This is called gravitational
force. E.g., In the solar system, planets orbit the Sun due to gravitation.
UNIVERSAL
LAW OF GRAVITATION
-
Every
object in the universe attracts every other object with a force proportional to
the product of their masses and inversely proportional to the square of the
distance between them. The force is along the line joining the centres of two
objects.
-
Let two
objects A and B of masses M and m lie at a distance d from
each other.
According
to the universal law of gravitation, the force F between two objects is
directly proportional to the product of their masses and inversely proportional
to the square of the distance between them.
- Where G is the constant of proportionality and is
called the universal gravitation constant.
-
The SI
unit of G is N m2 kg–2.
-
Henry Cavendish (1731 – 1810) found out the value of G using a sensitive balance. It
is 6.673 × 10–11 N m2 kg–2.
Example: Mass of the earth is 6 × 1024 kg and that of the moon is 7.4
× 1022 kg. If the distance between the earth and the moon is 3.84×105
km, calculate the force exerted by the earth on the moon. (G = 6.7 × 10–11
N m2 kg-2).
Solution:
Mass of the earth, M
= 6 × 1024 kg
Mass of the moon, m
= 7.4 × 1022 kg
Distance between earth
and moon, d = 3.84 × 105 km
= 3.84 × 105
× 1000 m
= 3.84 × 108 m
G = 6.7 × 10–11 N
m2 kg–2
= 2.02 × 1020 N.
IMPORTANCE
OF THE UNIVERSAL LAW OF GRAVITATION
It can explain several phenomena such as
(i)
the force
that binds us to the earth.
(ii)
the motion
of the moon around the earth.
(iii)
the motion
of planets around the Sun.
(iv)
the tides
due to the moon and the Sun.
FREE
FALL
-
When a
stone is thrown upwards, it reaches a certain height and then falls down.
-
If an
object falls towards the earth under gravitational force alone, it is called free
fall.
-
While falling,
the direction of motion remains unchanged. But the earth’s attraction causes a
change in the magnitude of velocity, leading to acceleration.
-
The
acceleration experienced during free fall due to the earth’s gravitational
force is called acceleration due to gravity (g). Its unit is ms–2.
-
According
to the second law of motion, F = m a.
- If the mass of the stone is m and acceleration due to gravity is g, the magnitude of the gravitational force F will be the product of mass & acceleration due to gravity.
M is the mass of the earth, and d is the distance between the object
and the earth.
- Let an object be on or near the surface of the earth. The distance d will be equal to R, the radius of the earth. Thus, for objects on or near the surface of the earth,
- The earth is not a perfect sphere. As the radius of the earth increases from the poles to the equator, the value of g becomes greater at the poles than at the equator. For most calculations, g can be considered constant on or near the earth. But for objects far from the earth, the acceleration due to gravity is given by g = G M /R2.
TO
CALCULATE THE VALUE OF g
Universal gravitational constant, G = 6.7 × 10–11 N m2
kg-2
Mass of the earth, M = 6 × 1024 kg
Radius of the earth, R = 6.4 × 106 m.
MOTION OF OBJECTS UNDER THE INFLUENCE OF GRAVITATIONAL
FORCE OF THE EARTH
Activity
•
Drop a
sheet of paper and a stone simultaneously from the first floor of a building.
•
The paper
falls slower than the stone due to air resistance, which is greater for the
paper than the stone. The air offers resistance due to friction to the motion of
the falling objects.
•
If the
experiment is conducted in a vacuum glass jar, the paper and the stone will
fall at the same rate.
-
It shows
that acceleration due to gravity is independent of its mass. i.e., all objects
fall at the same rate.
-
This was
proved by Galileo by dropping different objects from the top of the
Leaning Tower of Pisa in Italy.
-
As g
is constant near the earth, all the equations for the uniformly accelerated motion
of objects become valid with acceleration a replaced by g. The
equations are:
v = u + at s= ut + ½ at2 v2 = u2
+ 2as.
-
When
applying these equations, acceleration, a is positive if it is in the
direction of velocity (direction of motion) and negative when it opposes the
motion.
Problem: A car falls off a ledge and drops to the ground in 0.5 s. Let g
= 10 m s–2 (for simplifying the calculations).
(i)
What is
its speed on striking the ground?
(ii)
What is
its average speed during the 0.5 s?
(iii)
How high
is the ledge from the ground?
Solution:
Time, t = ½ second
Initial velocity, u = 0 m s–1
Acceleration due to gravity, g = 10 m s–2
Acceleration of the car, a = + 10 m s–2 (downward)
(i) speed v =
a t
v = 10 m s–2 × 0.5 s = 5
m s–1
|
(ii)
average speed = |
u + v |
|
2 |
= (0
m s–1+ 5 m s–1)/2 = 2.5
m s–1
(iii) distance travelled, s = ½ at2
= ½ × 10 m s–2
× (0.5 s)2
= ½ × 10 m s–2
× 0.25 s2 = 1.25 m
Thus height of the ledge from the
ground = 1.25 m.
Problem: An object is thrown vertically upwards
and rises to a height of 10 m. Calculate
(i) the velocity with which the object was thrown upwards. (ii) the time
taken by the object to reach the highest point.
Solution:
Distance travelled, s = 10 m
Final velocity, v = 0 ms–1
Acceleration due to gravity, g = 9.8 m s–2
Acceleration of the object, a = –9.8 m s–2 (upward
motion)
(i) v2 = u2 + 2as
0 = u2
+ 2 × (–9.8 m s–2) × 10 m
–u2
= –2 × 9.8 × 10 m2s–2
Initial velocity, u
= √196 m s-1 = 14 m s-1
(ii) v = u + a
t
0 = 14 ms–1
– 9.8 m s–2 × t
t = 1.43 s.
MASS
& WEIGHT
-
The mass
of an object is the measure of its inertia.
-
Greater the
mass, the greater is the inertia. It remains the same whether the object is on
the earth, the moon or in outer space. Thus, mass of an object is constant.
WEIGHT
-
The force
of attraction of the earth on an object is called the weight (W)
of the object.
-
Substituting
the Eq. F = m × g,
W = m × g
-
As the
weight is the force, its SI unit is newton (N).
-
The weight
is a force acting vertically downwards; it has both magnitude and direction.
-
The value
of g is constant at a given place. So, the weight is directly proportional
to the mass (m) of the object.
W α m
-
So, weight
can be used to measure mass at a given place.
-
Mass
remains constant, but weight varies with location due to changes in g.
WEIGHT OF AN OBJECT ON THE MOON
-
The weight
of an object on the moon is the force with which the moon attracts that object.
-
Mass of
the moon is less than that of the earth. So the moon exerts lesser force of
attraction on objects.
-
Applying
the universal law of gravitation, the weight of the object on the moon will be
-
Let the
weight of the same object on the earth be We. The mass of the
earth is M and its radius is R.
|
Celestial body |
Mass (kg) |
Radius (m) |
|
Earth |
5.98 × 1024 |
6.37 × 106 |
|
Moon |
7.36 × 1022 |
1.74 × 106 |
Problem: Mass of an object is 10 kg. What
is its weight on the earth?
Solution: Mass, m = 10 kg g
= 9.8 ms–2
Weight of the object, W = m × g
W = 10 kg × 9.8 ms-2
= 98 N.
Problem: An object weighs 10 N when measured
on the surface of the earth. What would be its weight when measured on the
surface of the moon?
Solution: Wm = (1/6) × We
|
i.e., Wm = |
We |
= |
10 |
N |
|
6 |
6 |
= 1.67 N.
THRUST
AND PRESSURE
-
The force
acting on an object perpendicular to the surface is called thrust. E.g.,
·
When
fixing a poster with a drawing pin, a force is directed perpendicular to the
surface of the board and acts on a smaller area at the tip of the pin.
·
Standing
on loose sand causes feet to sink due to the force (body weight) acting on a
small area (feet). When lie down, distributes the same force over a larger
area, preventing sinking.
Here, thrust is the same. But effects are different.
Therefore, the effect of thrust depends on the area on which it
acts. The effect of thrust on sand is larger while standing than while lying.
-
The thrust
on unit area is called pressure. Thus,
|
Pressure = |
Thrust |
|
Area |
-
The SI
unit of pressure= N/m² or N m⁻², or the pascal (Pa) in
honor of scientist Blaise Pascal.
Problem: A block of wood is kept on a tabletop. The mass of wooden block is
5 kg and its dimensions are 40 cm × 20 cm × 10 cm. Find the pressure exerted by
the wooden block on the table top if it is made to lie on the table top with
its sides of dimensions (a) 20 cm × 10 cm and (b) 40 cm × 20 cm.
Solution:
The mass of the wooden block = 5 kg
The dimensions = 40 cm × 20 cm × 10 cm
Here, the weight of the
wooden block applies a thrust on the table top. i.e., Thrust = F = m × g
= 5 kg × 9.8 ms–2
= 49 N
Area of a side = length × breadth
= 20 cm × 10 cm
= 200 cm2 = 0.02 m2
|
Pressure = |
Thrust |
= |
49 N |
|
Area |
0.02 m2 |
= 2450 N m-2.
When the block lies on
its side of dimensions 40 cm × 20 cm, it exerts the same thrust.
Area= length × breadth
= 40 cm × 20 cm
= 800 cm2 = 0.08 m2
|
Pressure = |
Thrust |
= |
49 N |
|
Area |
0.08 m2 |
= 612.5 N m–2
-
Thus, the
same force acting on a smaller area exerts a larger pressure, and a smaller pressure
on a larger area. This explains why a nail has a pointed tip, knives have sharp
edges and buildings have wide foundations.
A camel can run easily in a desert due to its wide, padded feet. These feet distribute the camel's weight over a larger area,
reducing pressure on the sand and preventing it from sinking.
An army tank rests upon a continuous
chain to distribute its weight over a larger area. This reduces pressure and
prevents the tank from sinking into soft terrain.
Trucks and buses have wider tires to distribute
their weight over a larger area.
This reduces pressure on the road and minimizes wear and tear.
PRESSURE
IN FLUIDS
-
All
liquids and gases are fluids.
-
A solid
exerts pressure on a surface due to its weight. Similarly, fluids also exert
pressure on the base and walls of the container in which they are enclosed.
-
Pressure exerted
in any confined mass of fluid is transmitted undiminished in all directions.
BUOYANCY
-
It is the tendency of an object to float in a fluid.
Activity
•
Place an empty plastic bottle (closed with an airtight stopper) in a
bucket of water. The bottle floats.
•
Push the bottle down into the water. An upward force is felt, and it
becomes harder to push further. This indicates that water exerts an increasing
upward force as the bottle is pushed deeper until fully immersed.
•
Release the bottle, and it bounces back to the surface.
-
The
gravitational force acts downward on the bottle, pulling it down. Meanwhile,
the water exerts an upward force, pushing the bottle up. Since the buoyant
force exerted by the water is greater than the bottle's weight, the bottle
rises when released.
-
To keep
the bottle completely immersed, the upward force must be balanced by a downward
external force. This force must at least be equal to the difference between the
upward force and the weight of the bottle.
-
The upward
force exerted by a fluid on an immersed object is called upthrust or buoyant
force. This makes the object feel lighter and helps it float. E.g.,
·
Swimming
in a pool makes the body feel lighter.
·
A bucket
of water feels lighter underwater but heavier when lifted out.
·
A ship
made of iron and steel floats on water.
WHY
OBJECTS FLOAT OR SINK WHEN PLACED ON THE SURFACE OF WATER?
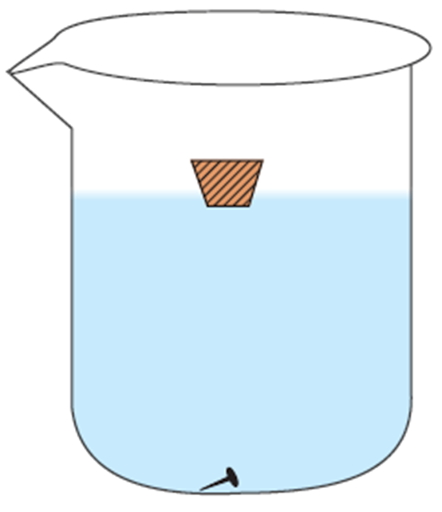
- Place
an iron nail on the surface of water in a beaker. The nail sinks because the
downward gravitational force on the nail is greater than the upward buoyant
force exerted by the water.
-
Take a
piece of cork and an iron nail of equal mass. Place them on water. The cork
floats and the nail sinks.
-
It is due
to the difference in their densities. Density of a substance is defined as the mass
per unit volume.
-
The
magnitude of buoyant force depends on the density of the fluid.
-
Density of
cork is less than that of water. i.e., upthrust of water is greater than the
weight of cork. So it floats.
-
Density of
nail is more than that of water. i.e., upthrust of water is less than the
weight of the nail. So it sinks.
-
Objects
with lower density than a liquid float. Objects with greater density than a
liquid sink.
-
A ship
floats on water because its overall density, including the air inside it, is
less than the density of water. It displaces more water, generating enough
buoyant force to support its weight. A sheet of metal sinks because it has a
higher density and displaces less water, generating insufficient buoyant force.
ARCHIMEDES’
PRINCIPLE
Activity
•
Tie a stone to a rubber string / spring balance
and suspend.
•
The
elongation of the string or reading on the balance increases due to the stone's
weight.
•
As the
stone is slowly dipped in water, the elongation of the string or reading on the
balance decreases. However, no further change is observed once the stone gets
fully immersed in the water.
-
The
elongation is caused by the weight of the stone. When the stone is lowered into
water, the extension decreases, indicating that an upward force (buoyant force)
is acting on the stone. This reduces the net force on the string, causing the
elongation to decrease.
-
Magnitude
of buoyant force, its variation in different fluids etc. are explained by
Archimedes' principle.
-
Archimedes’
principle: Proposed by Archimedes (a Greek
scientist). When a body is immersed fully or partially in a fluid, it
experiences an upward force that is equal to the weight of the fluid displaced by
it.
-
The
elongation of the string does not decrease further once the stone becomes fully
immersed in water because the buoyant force reaches its maximum when the body
displaces the maximum amount of fluid. Beyond this point, the buoyant force
remains constant, so the elongation stays the same.
- Applications of Archimedes’ principle:
·
It is used
in designing ships and submarines.
·
Lactometers (to determine the purity of milk) and Hydrometers (to determine density of liquids) are based on this principle.
👉 View PDF